MATLAB Filter Designer 工具教程（filterDesigner fdatool）

本文最后更新于：2025年12月9日 凌晨

MATLAB Filter Designer 工具教程

  MATLAB 的 Filter Designer 是一个用于数字滤波器设计与分析的可视化工具，它为工程师和研究者提供了一个无需编写代码即可快速构建 FIR 和 IIR 滤波器的平台。通过该工具，用户能够直观地设置滤波器类型、截止频率、阶数、窗函数或经典模拟原型等关键参数，并实时查看幅频响应、相频响应、群延迟、零极点图等特性，从而高效完成滤波器的性能评估与优化。Filter Designer 同时支持将设计结果以滤波器对象或系数形式导出到 MATLAB 工作区，还能自动生成相应的 MATLAB 代码，便于模型复现、批处理以及集成到后续的信号处理流程中。此外，该工具还具备定点滤波器设计与量化分析能力，可用于 DSP、FPGA 等嵌入式系统的滤波器实现，是数字信号处理领域学习、实验和工程应用的重要辅助工具。

一、Filter Designer 是什么？

MATLAB 的 Filter Designer（旧称 fdatool）是一个图形化数字滤波器设计工具，可用于设计：

  • FIR / IIR 滤波器
  • 低通、高通、带通、带阻
  • 多速率滤波器
  • 幅频响应、相频响应、群延迟分析

适合信号处理、嵌入式、通信和音频工程。

二、如何打开 Filter Designer

使用命令：

1
filterDesigner

Apps → Signal Processing → Filter Designer

三、MATLAB Filter Designer 界面结构

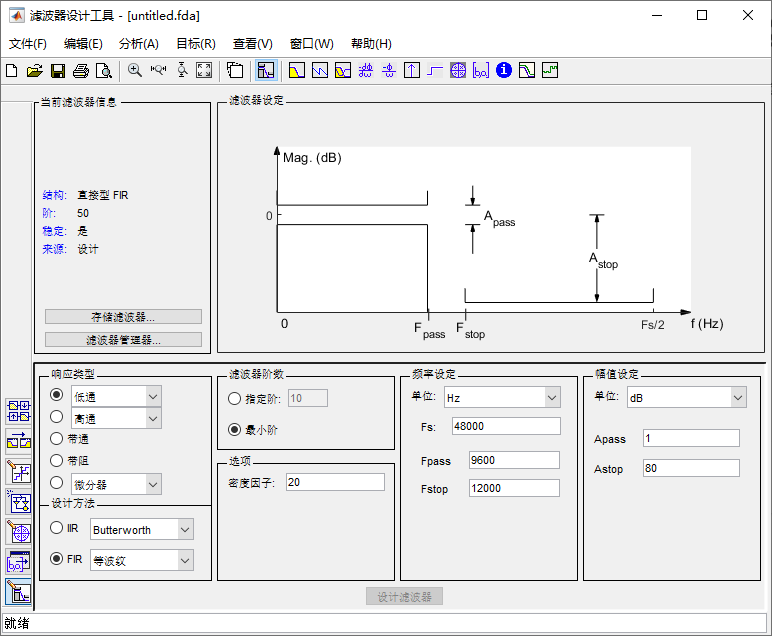
MATLAB Filter Designer 界面

3.1 当前滤波器信息

3.1.1 滤波器的结构类型（直接型FIR）

📌 说明：

  • 当前滤波器是 FIR（有限冲激响应）
  • 使用最基本、最常用的 直接形式（Direct Form）实现

👉 使用意义： 这个结构会决定后续你在 MCU/DSP/FPGA 中实现滤波器的方式，尤其是一阶式、二阶式、全系数方式等。

3.1.2 当前滤波器的阶数

📌 说明：

滤波器阶数 = 数字滤波器系数的数量 - 1 例如 50 阶 FIR → 有 51 个滤波器系数（taps）

👉 使用意义：你要重点关注的参数！

  • 越高阶 → 滤波器越陡峭 → 运算量越大
  • FIR 阶数影响 CPU 使用率、延迟、功耗
  • MCU/FPGA 中必须评估是否能跑得动

3.1.3 滤波器是否稳定

📌 对于 FIR → 一定稳定 （因为没有反馈环）

若是 IIR 就非常关键：

  • 稳定：极点在单位圆内
  • 不稳定：极点超出单位圆，会输出发散的震荡波形！

👉 使用意义：

如果你设计的是 IIR 滤波器，要看这里是否标“是”，否则滤波器不能用！

3.1.4 滤波器的来源

📌表示当前滤波器的来源是：

  • 由你在 FilterDesigner 中设计的（Design）
  • 或从 MAT 文件导入的（Import）
  • 或通过 Filter Manager 替换加载的

👉 使用意义：

如果你从文件加载了其他滤波器，这里会显示来源不同，帮助你确认当前正在编辑哪一个滤波器对象。

3.1.5 【按钮】存储滤波器

📌 点击后可选择：

  • 保存为 MAT 文件
  • 保存为滤波器对象（dfilt / dsp.FIRFilter）
  • 保存系数（b/a、SOS 等）

👉 工程中最常用的用途：

  • 导出滤波器给 MATLAB 脚本使用

  • 导出给 Simulink

  • 导出给嵌入式 C 程序（生成 C 代码）

  • 导出为 coefficient vector b[]

3.1.6 【按钮】滤波器管理器

这个按钮可以打开 Filter Manager，用于：

  • 比较多个滤波器
  • 并行存储多个不同设计的版本
  • 选择最优响应
  • 切换不同滤波器进行对比与导出

📌 工程用途非常大：

例如你设计多个：

  • 不同阶数
  • 不同过渡带宽
  • 不同 IIR/FIR 方法

你可以存到 Filter Manager 然后逐一比较频率响应。

3.2 滤波器设定（信息展示）

对应设计滤波器必须输入的 4 类参数，同时展示：

  • 采样率 Fs（因此右端是 Fs/2，也就是奈奎斯特频率）
  • 纵轴是幅度（以 dB 为单位）

它帮助你理解滤波器目标的“形状”。

通带截止频率 Fpass

含义：

在这个频率之前，信号应尽量保持不衰减（保持接近 0 dB）。

通常要求：

  • 通带范围内的信号变化 ≤ Apass（例如 0.5 dB 或 1 dB）

阻带起始频率 Fstop

含义：

在 Fstop 之后，信号必须被强烈衰减。

图中右边的下沉线表示阻带开始。阻带范围：

  • Fstop 到 Fs/2

通带最大衰减 Apass

含义：

在通带范围内，允许的最大衰减（或纹波）。

例如：

  • Apass = 1 dB → 通带幅度可以在 -1 dB 以内浮动
  • Apass 越小 → 通带越平坦 → 滤波器阶数会上升

阻带最小衰减 Astop

含义：

阻带中信号必须至少衰减多少 dB。

例如：

  • Astop = 40 dB → 阻带信号降低 100 倍
  • Astop 越大 → 抑制越强 → 阶数会明显增加

3.3 响应类型

  • 低通

  1. 升余弦
  2. 半带低通
  3. 奈奎斯特
  4. 反正弦低通

  • 高通

  1. 半带高通
  2. 反正弦高通

  • 带通

  • 带阻

  • 微分器

  1. 多频带
  2. Hilbert 变换器
  3. 任意幅值
  4. 任意群延迟
  5. 峰值
  6. 陷波

3.4 设计方法

3.4.1 IIR

  • Butterworth
  • Chebyshev I 型
  • Chebyshev II 型
  • 圆
  • 最小 P-范数
  • 约束最小 P-范数

3.4.2 FIR

  • 等波纹
  • 最小二乘
  • 窗
  • 约束最小二乘
  • 复等波纹
  • 最小 P-范数
  • 约束等波纹
  • 广义等波纹
  • 约束频带等波纹
  • 插值 FIR

3.5 滤波器阶数

3.5.1 ✔ 适用“指定阶数”的情况

选择 指定阶数 如果你是：

  • 运行平台是 MCU（如 STM32）
  • 运行在 DSP（如 TI C6000）
  • 采样率高（数百 kHz ~ MHz）
  • FPGA 设计需要固定资源
  • 想要控制延迟
  • 想要统一硬件延迟（如并行滤波器）

你可以手动试多个阶数，看是否满足频率要求。

3.5.2 ✔ 适用“最小阶数”的情况

选择 最小阶数（自动阶数）如果你是：

  • 信号处理算法研究
  • MATLAB 仿真优先
  • PC 运行，不考虑实时性
  • 对通带/阻带要求严格
  • 想要尽可能好的效果

MATLAB 会返回一个满足你规格的最低阶滤波器。

阶数对滤波器的影响

项目 阶数高 阶数低
通带平坦度 好 差
阻带抑制 好 差
过渡带宽度 窄 宽
运算量 大 小
延迟 大 小
实时性 低 高
对 MCU/FPGA 负担 大 小

3.6 频率设定

在 Filter Designer 中，不同的滤波器类型（低通/高通/带通/带阻）会对应不同的频率字段：

你截图中的字段属于 微分器或 Hilbert 滤波器类，只有：

  • Fs：采样频率
  • Fc：截止频率（Cutoff Frequency）

而一般低通、高通等会出现：

  • Fpass（通带截止）
  • Fstop（阻带起始）

你这里之所以显示 Fc，是因为你选择的“响应类型”只有一个关键频率。

采样率的作用：

  • 直接决定奈奎斯特频率（Fs/2 = 24000 Hz）
  • 决定滤波器频率范围
  • 所有频率参数都基于 Fs（包括 Fpass/Fstop/Fc）

如果你 Fs 设置错误：

  • 截止点会错
  • 生成完全错误的滤波器

这是最需要确保正确填写的参数。

3.7 幅值设定

Butterworth 滤波器的截止频率（Cutoff Frequency）定义为幅度下降 -3 dB 的位置。

特性 FIR IIR
是否有反馈 ❌ 无反馈 ✅ 有反馈
是否绝对稳定 ✅ 是 ❌ 需分析极点
相位响应 ⭐ 可线性相位 ❌ 非线性相位
阶数 高（几十到几千） 低（3~16 阶常见）
计算量 大 小
内存占用 大 小
适用于高采样率滤波 差 优秀
实现复杂度 低 中等
实现风险 小 可能出现溢出、震荡
用于音频 优 可但会失真
用于控制系统 次选 优先选
DSP 场景 广泛 高速场景常用
MCU 场景 中 非常适合
FPGA 场景 中 非常适合
类型 数字差分方程（核心） 关键特点
FIR（有限冲激响应） 仅包含输入延迟项： 无反馈、一定稳定、线性相位可实现
IIR（无限冲激响应） 包含输入 & 输出项：$ y[n] = {k=0}^{M} b_k x[n-k] - {k=1}^{N} a_k y[n-k] $ 有反馈、可能不稳定、阶数低、相位非线性

3.8 转换结构

因为 相同的滤波器（相同的 b/a 系数）可以用不同的算法结构实现。

所有结构都会得到相同的幅频与相频响应，只是内部实现方式不同：

  • 有的更稳定
  • 有的需要更少的存储单元
  • 有的更适合实时系统
  • 有的适合 FPGA
  • 有的更适合定点实现

换句话说：

结构 = 数字滤波器的内部实现方式，而不是滤波器本身。

类型 优点 缺点
IIR/FIR Direct Form 易懂，通用 高频滤波器组难以稳定
SOS（二阶节） 稳定，嵌入式常用 难构造滤波器组
CA（耦合全通） 自然构造互补滤波器 结构更复杂
PC-CA（功率互补 + 耦合全通） 完全能量保持、完美互补 用途专门，不适用于一般场景
PC-CA Lattice（格型） 最稳的全通滤波器实现 系数含义非直观

3.8.1 Direct-Form I, SOS（直接型 I + 二阶节）

最经典，最直观，有前馈 + 反馈两个独立延迟链。

特点：

  • 两条延时链：一条用于 x，一条用于 y
  • 最直观、易理解
  • 更适合浮点系统（MATLAB / PC）
  • 不适合定点（量化后不太稳定）

适合：

  • 分析、验证

  • MATLAB 仿真

  • 浮点 DSP

3.8.2 Direct-Form II, SOS（直接型 II + 二阶节）

最节省内存的结构（双线性合并延时）。

特点：

  • 只有一个延时链（合并 x 和 y 的延时）
  • 内部态变量容易溢出
  • 定点实现数值不稳定风险高
  • 浮点系统可用

适合：

  • DSP 浮点平台
  • 内存受限场景（延迟最少）

3.8.3 Direct-Form I Transposed, SOS（转置直接型 I）

数值更稳定，误差传播小。

特点：

  • 对 Direct-Form I 的数值特性进行改善
  • 除了滤波器输出处外，添加反馈前置
  • 量化噪声传播方向更有利
  • 对高阶 IIR 更稳定

适合：

  • MCU
  • DSP（定点/浮点）
  • 稳定性优先的场景

3.8.4 Direct-Form II Transposed, SOS（转置直接型 II）

目前 MCU / DSP / FPGA 最常用的 IIR 二阶节结构。

这是业界标准的 "biquad" 结构。

特点：

  • 计算效率高
  • 仅需 2 个状态变量
  • 稳定性优于 Direct Form II 原始结构
  • 定点/浮点均适用
  • 对 SOS（二阶节）非常稳定

适合：

  • STM32 / DSP / ARM
  • FPGA
  • 高可靠实时系统
  • 高阶 IIR 分解为 SOS 后逐节实现

如果用户不知道选哪个 → 99% 情况应该选“Direct-Form II Transposed, SOS”。

3.8.5 ARMA（移动自回归平均滤波器）格型

ARMA 即： 也就是一般 IIR 的数学模型形式。

意义：

  • 用于系统辨识
  • 用于基于信号模型的滤波
  • 通常不用于直接硬件实现

3.8.6 耦合全通（CA）格型

CA = Complex Allpass filters（复全通滤波器）。

用于：

  • 相位补偿
  • 高保真音频
  • 变速不变调（time-scale modification）
  • Hilbert 滤波器

较少用于一般工程。

3.8.7 具有功率互补(PC)输出的耦合全通(CA)格型

PC = Phase-Corrected，全通相位修正结构。

用于：

  • 高级音频处理
  • 语音信号质量增强
  • 变速变调算法
  • 精确相位操控

一般信号处理应用用不到。

3.9 转换单节（转换为二阶节）

3.9.1 单节滤波器（single-section）

就是直接用一组 完整的 b 系数（分子）与 a 系数（分母） 来表示滤波器： 例如 6 阶 IIR（N=6）用一个式子表示：

1
2
b = [b0 b1 b2 b3 b4 b5 b6]
a = [1 a1 a2 a3 a4 a5 a6]

这种结构称为 Direct-Form（直接型） 或 单节结构。

3.9.2 二阶节（Second Order Section）

把一个高阶 IIR（如 6、8、10 阶）分解为多个 2 阶滤波器的串联。

例如 6 阶 IIR： 每个二阶节： MATLAB 中一个 SOS 行对应一个二阶节：

1
2
3
4
5
6
SOS = [
 b01 b11 b21  a01 a11 a21
 b02 b12 b22  a02 a12 a22
 b03 b13 b23  a03 a13 a23
];
G = [g1 g2 g3];

3.9.3 为什么要用 SOS？（数值稳定性）

项目 单节（b/a 形式） SOS（二阶节）
稳定性 ❌ 差 ✔ 最佳
数值精度敏感性 高 低
算法结构 Direct-form Biquad（行业标准）
嵌入式实现 不推荐 ✔ 强烈推荐
FPGA 难实现 ✔ 每节独立，可流水线
MATLAB Filter Designer 默认输出 单节 ✔ 默认用 SOS（IIR 时）

数值稳定性对比（重点！）

3.9.3.1 ✔ 单节结构：
  • a 系数随阶数剧烈变化
  • 系数差异可能达 10⁶ 倍
  • 固有病态
  • 定点/浮点都风险高
  • 容易出现：
    • 输出爆炸
    • 抖动
    • 噪声放大
    • 对量化敏感

尤其阶数 ≥ 4 的时候。

3.9.3.2 ✔ SOS 结构：
  • 每节只有 2 阶，极点/零点成对
  • 系数范围小且稳定
  • 误差不累积
  • 定点 / 浮点平台都可靠
  • 工业标准做法

DSP、STM32、FPGA 等嵌入式实现 IIR 时，都必须用 SOS（biquad）。

3.10 FIR 数字差分方程

FIR：有限长冲激响应（长度 M+1）： 特点：

  • 只有输入的过去值
  • 是 FIR 系数（taps）
  • 一定稳定
  • 容易设计成线性相位

3.11 IIR 数字差分方程

IIR：具有反馈项： 其中：

  • b_k：前馈系数
  • a_k：反馈系数
  • a₀ = 1（通常归一化）

四、二阶Butterworth低通滤波器设计示例

1️⃣ 设计指标

  • 滤波器类型：IIR，Butterworth
  • 阶数：2 阶
  • 采样频率：Fs = 1000 Hz
  • 截止频率：Fc = 40 Hz（-3 dB 处）

归一化截止频率：

2️⃣ MATLAB 设计代码

1
2
3
4
5
6
7
8
9
10
11
Fs = 5000;          % 采样频率
Fc = 40;            % 截止频率 40 Hz

Wn = Fc / (Fs/2);   % 归一化截止频率 0~1

% 二阶 Butterworth 低通
[b, a] = butter(2, Wn, 'low');

% 看看频率响应
freqz(b, a, 1024, Fs);
grid on;

在我这边算出的系数为（保留 8 位小数）：

1
2
b = [0.01335920  0.02671840  0.01335920]
a = [1.00000000 -1.64745998  0.70089678]

和你之前代码里的系数非常接近，是同一类设计结果。

3️⃣ 差分方程形式

对应的数字滤波器差分方程： 按照标准 IIR 写法（把 a1,a2 视为正号参数）： 其中：

1
2
3
4
5
b0 = 0.01335920
b1 = 0.02671840
b2 = 0.01335920
a1 = -1.64745998
a2 =  0.70089678

4️⃣ C/STM32 中的直接实现示例（Direct Form I）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 二阶 IIR 状态，使用数组存储延迟项：
// x[0] = x[n-1], x[1] = x[n-2]
// y[0] = y[n-1], y[1] = y[n-2]
typedef struct {
    float x[ 2 ];
    float y[ 2 ];
} IIR2_State;

static IIR2_State iir_lp = { { 0, 0 }, { 0, 0 } };

// 二阶低通滤波器一步计算
float IIR_LP40Hz_Step( float x ) {
    // 分子系数 b0 b1 b2
    const float b[ 3 ] = { 0.01335920f, 0.02671840f, 0.01335920f };

    // 分母系数 a1 a2（a0=1 不存）
    const float a[ 3 ] = { 1.0f, -1.64745998f, 0.70089678f };
    // a[0]=a0=1，a[1]=a1，a[2]=a2

    // IIR 计算（Direct Form I）
    float y = b[ 0 ] * x + b[ 1 ] * iir_lp.x[ 0 ] + b[ 2 ] * iir_lp.x[ 1 ] - a[ 1 ] * iir_lp.y[ 0 ] - a[ 2 ] * iir_lp.y[ 1 ];

    // 状态更新
    iir_lp.x[ 1 ] = iir_lp.x[ 0 ];
    iir_lp.x[ 0 ] = x;

    iir_lp.y[ 1 ] = iir_lp.y[ 0 ];
    iir_lp.y[ 0 ] = y;

    return y;
}

如果你想用 SOS/biquad（Direct Form II Transposed），就可以把这组 b,a 再用 tf2sos 分成一节，按我们前面聊过的 biquad 模板来写。

5️⃣ 在 Filter Designer 里的操作（GUI）

  1. filterDesigner 打开工具
  2. 响应类型：低通
  3. 设计方法：IIR → Butterworth
  4. 滤波器阶数：选择“指定阶”，填 2
  5. 频率设置：Fs = 1000，Fc = 40（或 Fpass=40）
  6. 点击“设计滤波器（Design Filter）”
  7. File → Export… 导出 b, a 或 SOS 系数即可

五、二阶 IIR Notch 陷波滤波器设计示例

MATLAB 设计代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
%% 二阶 IIR Notch 带阻滤波器设计
Fs = 5000;   % 采样频率 (Hz)
F0 = 6;      % 陷波中心频率 (Hz)
BW = 1;      % 带宽 (Hz，3 dB 带宽)

% 归一化频率（相对于 Nyquist 频率 Fs/2）
wo = F0 / (Fs/2);    % 归一化中心频率 (0~1)
bw = BW / (Fs/2);    % 归一化带宽

% 设计二阶 IIR Notch 带阻滤波器
[b, a] = iirnotch(wo, bw);

% 打印滤波器系数
disp('分子系数 b = '); disp(b);
disp('分母系数 a = '); disp(a);
Matlab
高通 低通 Matlab IIR FIR

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！